This package is divided in three parts:
The function hierarchy is an abstract hierarchy which defines meta-function in the sense that the user has to derive from these classes to define its real function.
struct MyLinearFunction : public LinearFunction { //FIXME: some code is missing }; struct MyDerivableFunction : public DerivableFunction { //FIXME: some code is missing }; // etc...
The user can defines as many functions as he wants as long as he respects the constraints defined by the classes he inherits from:
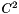 ) has a hessian.
) has a hessian. 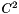 function.
function. It is important to note that all these functions are 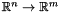 functions.
functions.
These functions have to be considered as m functions from to  . In particular, it means that in the gradient/hessian methods, the second argument (integer) refers to which function you want to get the gradient/hessian.
. In particular, it means that in the gradient/hessian methods, the second argument (integer) refers to which function you want to get the gradient/hessian.
It avoids useless computations when the whole Jacobian is not needed. Hence, it also avoid the use of a tensor as this structure is particularly costly and not built-in in Eigen (the matrix library the package rely on).
This set of meta-functions is completed by two generic implementations of quadratic and linear functions in respectively NumericQuadraticFunction and NumericLinearFunction. Those are real functions as the user is meant to instantiate them, not derive from them.
The problem class defines a complete optimization problem. It is composed of:
 cost (or objective) function.
cost (or objective) function. The problem class is templated by two parameters:
Those two parameters defines a class of problem. For instance, QP solves problems where the objective function is quadratic and the constraints are linear.
To a class of problem matches a set of solvers designed to exactly those problems.
The copy constructor of the Problem class allows to make the problem more generic by replacing F or C by a more general type.
Examples:
Ie: you can always go higher in the function hierarchy but you can not go deeper.
However, this transformation as any dynamic typing makes forget specific information and might slow-down the process. Ie: solving a linear problem as a non-linear one is slower than directly solving it.
The solver hierarchy is divided in three parts:
The generic solver is an abstract class which is the root of the hierarchy. All the solvers have to inherit from this class directly or indirectly.
It only defines three methods:
solve (virtual pure) getMinimum reset The method solve has to fill the protected attribute result_. It is implemented by the bridges at the bottom of the hierarchy.
By default result_ contains an instance the No_Solution class. It has to be changed to an instance of Result, ResultWithWarnings or SolverError.
No_Solution: represents the fact that solve has never been called. A user should never retrieve an instance of No_Solution. Result, ResultWithWarnings: represents a valid result. If ResultWithWarnings is used, some non-critical problem might have happened and are specified in the object (minor numerical instabilities for instance). SolverError: indicate that the optimization has failed. The solve method should rarely be called by the user. Instead, the user calls getMinimum which calls solve if required. If getMinimum is called several time, the problem is only solved once.
The reset method should be called when one wants to manually force the recomputation of the solution.
The Solver class is parametrized by two parameters as the Problem class. It defines an abstract solver for a class of optimization problems.
For instance, a QP should inherit from Solver<QuadraticFunction, LinearFunction>.
This level of the hierarchy integrates the notion of Problem, hence the problem method is defined to access the problem. Once a solver is created with a problem, the problem can never be modified again.
The leafs of the hierarchy are bridges. The role of a bridge is to convert the generic representation of the problem into the solver's representation. It might also emulate some missing features of the back-end solver.
A bridge mainly implements the solve method. It may also exposes the underlying solver's internal mechanism for fine tuning.