Building the problem and solving it.
A capsule can be uniquely defined by its two main axis end points 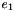 and
and 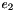 , as well as its radius
, as well as its radius 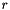 . To compute the minimum-volume bounding capsule over one or more polyhedrons, an non-linear optimization problem is defined, then solved using a jacobian-based numerical optimization solver provided through RobOptim and an IPOPT plugin.
. To compute the minimum-volume bounding capsule over one or more polyhedrons, an non-linear optimization problem is defined, then solved using a jacobian-based numerical optimization solver provided through RobOptim and an IPOPT plugin.
The problem that will be solved is:
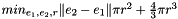
subject to:
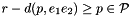
This ensures that the minimum-volume capsule is found while all points of the set 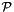 , which represents one or more polyhedrons, all lie inside the capsule.
, which represents one or more polyhedrons, all lie inside the capsule.
Building the problem and solving it.
This part of the tutorial covers how to compute an optimal capsule. The steps are:
- Instanciate or load a polyhedron. Here we create a simple cube.
BOOST_AUTO_TEST_CASE (fitter)
{
using namespace roboptim::capsule;
polyhedron.push_back (
point_t (-halfLength, -halfLength, -halfLength));
polyhedron.push_back (
point_t (-halfLength, -halfLength, halfLength));
polyhedron.push_back (
point_t (-halfLength, halfLength, -halfLength));
polyhedron.push_back (
point_t (-halfLength, halfLength, halfLength));
polyhedron.push_back (
point_t (halfLength, -halfLength, -halfLength));
polyhedron.push_back (
point_t (halfLength, -halfLength, halfLength));
polyhedron.push_back (
point_t (halfLength, halfLength, -halfLength));
polyhedron.push_back (
point_t (halfLength, halfLength, halfLength));
polyhedrons.push_back (polyhedron);
- Compute the convex hull of one or more polyhedrons. This offers the nice property that a lower number of constraints will be added to the optimization problem without affecting the result.
- Instanciate a fitter. This is the main class in this package and is used to find the best fitting capsule over the input polyhedron vector.
Fitter fitter (convexPolyhedrons);
- Set initial parameters for the fitter. One very nice way to find a good initial guess is to compute a bounding capsule with least-squares method. This way, the initial capsule enforces all constraints and is not too far from the optimum.
endPoint1, endPoint2, radius);
- Run the solver and retrieve the optimal capsule parameters.
fitter.computeBestFitCapsule (initParam);
argument_t solutionParam = fitter.solutionParam ();
std::cout << fitter << std::endl;
}
To see more usage examples, consider looking at the test directory of the project which contains the project's test suite.
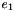 and
and 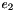 , as well as its radius
, as well as its radius 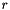 . To compute the minimum-volume bounding capsule over one or more polyhedrons, an non-linear optimization problem is defined, then solved using a jacobian-based numerical optimization solver provided through RobOptim and an IPOPT plugin.
. To compute the minimum-volume bounding capsule over one or more polyhedrons, an non-linear optimization problem is defined, then solved using a jacobian-based numerical optimization solver provided through RobOptim and an IPOPT plugin.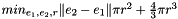
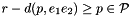
 , which represents one or more polyhedrons, all lie inside the capsule.
, which represents one or more polyhedrons, all lie inside the capsule.