Solving a problem is done through several steps:
The following example defines a cost function F and two constraints G0 and G1.
The problem that will be solved in this tutorial is the 71th problem of Hock-Schittkowski:
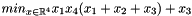
with the following constraints:
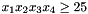
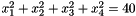
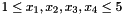
The library contains the following hierarchy of functions:
These types correspond to dense vectors and matrices relying on Eigen. RobOptim also support dense matrices and you can even extend the framework to support your own types.
When defining a new function, you have to derive your new function from one of those classes. Depending on the class you derive from, you will be have to implement one or several methods:
It is usually recommended to derive from the deepest possible class of the hierarchy (deriving from TwiceDerivableFunction is better than DerivableFunction).
Keep in mind that the type of the function represents the amount of information the solver will get, not the real nature of a function (it is possible to avoid defining a hessian by deriving from DerivableFunction, even if you function can be derived twice).
In the following sample, a TwiceDerivableFunction will be defined.
struct F : public TwiceDerivableFunction { F () : TwiceDerivableFunction (4, 1) { } void impl_compute (result_t& result, const argument_t& x) const throw () { result (0) = x[0] * x[3] * (x[0] + x[1] + x[2]) + x[3]; } void impl_gradient (gradient_t& grad, const argument_t& x, int) const throw () { grad[0] = x[0] * x[3] + x[3] * (x[0] + x[1] + x[2]); grad[1] = x[0] * x[3]; grad[2] = x[0] * x[3] + 1; grad[3] = x[0] * (x[0] + x[1] + x[2]); } void impl_hessian (hessian_t& h, const argument_t& x, int) const throw () { h (0, 0) = 2 * x[3]; h (0, 1) = x[3]; h (0, 2) = x[3]; h (0, 3) = 2 * x[0] + x[1] + x[2]; h (1, 0) = x[3]; h (1, 1) = 0.; h (1, 2) = 0.; h (1, 3) = x[0]; h (2, 0) = x[3]; h (2, 1) = 0.; h (2, 2) = 0.; h (2, 3) = x[1]; h (3, 0) = 2 * x[0] + x[1] + x[2]; h (3, 1) = x[0]; h (3, 2) = x[0]; h (3, 3) = 0.; return h; } };
A constraint is no different from a cost function and can be defined in the same way than a cost function.
The following sample defines two constraints which are twice derivable functions.
struct G0 : public TwiceDerivableFunction { G0 () : TwiceDerivableFunction (4, 1) { } void impl_compute (result_t& result, const argument_t& x) const throw () { result (0) = x[0] * x[1] * x[2] * x[3]; } void impl_gradient (gradient_t& grad, const argument_t& x, int) const throw () { grad[0] = x[1] * x[2] * x[3]; grad[1] = x[0] * x[2] * x[3]; grad[2] = x[0] * x[1] * x[3]; grad[3] = x[0] * x[1] * x[2]; } void impl_hessian (hessian_t& h, const argument_t& x, int) const throw () { h (0, 0) = 0.; h (0, 1) = x[2] * x[3]; h (0, 2) = x[1] * x[3]; h (0, 3) = x[1] * x[2]; h (1, 0) = x[2] * x[3]; h (1, 1) = 0.; h (1, 2) = x[0] * x[3]; h (1, 3) = x[0] * x[2]; h (2, 0) = x[1] * x[3]; h (2, 1) = x[0] * x[3]; h (2, 2) = 0.; h (2, 3) = x[0] * x[1]; h (3, 0) = x[1] * x[2]; h (3, 1) = x[0] * x[2]; h (3, 2) = x[0] * x[1]; h (3, 3) = 0.; } }; struct G1 : public TwiceDerivableFunction { G1 () : TwiceDerivableFunction (4, 1) { } void impl_compute (result_t& result, const argument_t& x) const throw () { result (0) = x[0]*x[0] + x[1]*x[1] + x[2]*x[2] + x[3]*x[3]; } void impl_gradient (gradient_t& grad, const argument_t& x, int) const throw () { grad[0] = 2 * x[0]; grad[1] = 2 * x[1]; grad[2] = 2 * x[2]; grad[3] = 2 * x[3]; } void impl_hessian (hessian_t& h, const argument_t& x, int) const throw () { h (0, 0) = 2.; h (0, 1) = 0.; h (0, 2) = 0.; h (0, 3) = 0.; h (1, 0) = 0.; h (1, 1) = 2.; h (1, 2) = 0.; h (1, 3) = 0.; h (2, 0) = 0.; h (2, 1) = 0.; h (2, 2) = 2.; h (2, 3) = 0.; h (3, 0) = 0.; h (3, 1) = 0.; h (3, 2) = 0.; h (3, 3) = 2.; } };
The last part of this tutorial covers how to build a problem and solve it. The steps are:
int run_test () { F f; G0 g0; G1 g1; solver_t::problem_t pb (f); // Set bound for all variables. // 1. < x_i < 5. (x_i in [1.;5.]) for (Function::size_type i = 0; i < pb.function ().n; ++i) pb.argBounds ()[i] = T::makeBound (1., 5.); // Add constraints. pb.addConstraint (&g0, T::makeUpperBound (25.)); pb.addConstraint (&g1, T::makeBound (40., 40.)); // Set the starting point. Function::vector_t start (pb.function ().n); start[0] = 1., start[1] = 5., start[2] = 5., start[3] = 1.; initialize_problem (pb, g0, g1); // Initialize solver. // Here we are relying on the Ipopt solver (available separately). // You may change this string to load the solver you wish to use. SolverFactory<solver_t> factory ("ipopt-td", problem); solver_t& solver = factory (); // Compute the minimum and retrieve the result. solver_t::result_t res = solver.minimum (); // Display solver information. std::cout << solver << std::endl; // Check if the minimization has succeed. switch (solver.minimumType ()) { case SOLVER_NO_SOLUTION: std::cerr << "No solution." << std::endl; return 1; case SOLVER_ERROR: std::cerr << "An error happened: " << solver.getMinimum<SolverError> ().what () << std::endl; return 2; case SOLVER_VALUE_WARNINGS: { // Get the ``real'' result. Result& result = solver.getMinimum<ResultWithWarnings> (); // Display the result. std::cout << "A solution has been found (minor problems occurred): " << std::endl << result << std::endl; return 0; } case SOLVER_VALUE: { // Get the ``real'' result. Result& result = solver.getMinimum<Result> (); // Display the result. std::cout << "A solution has been found: " << std::endl; std::cout << result << std::endl; return 0; } } // Should never happen. assert (0); return 42; }
This is the last piece of code needed to instantiate and resolve an optimization problem with this package.
To see more usage examples, consider looking at the test directory of the project which contains the project's test suite.