roboptim::NTimesDerivableFunction< 2 > Class Template Reference

Explicit specialization for the stop case of NTimesDerivable class. More...

#include <roboptim/core/n-times-derivable-function.hh>

Inheritance diagram for roboptim::NTimesDerivableFunction< 2 >:

Collaboration diagram for roboptim::NTimesDerivableFunction< 2 >:

List of all members.

Public Member Functions
virtual size_type	derivabilityOrderMax () const
	Returns the maximum derivability order (relevant for N>2 only)
virtual	~NTimesDerivableFunction () throw ()
size_type	derivativeSize () const throw ()
	Return the size of the derivative vector.
bool	isValidDerivative (const gradient_t &derivative) const throw ()
	Check if a derivative is valid (check sizes).
result_t	operator() (double argument) const throw ()
	Evaluate the function at a specified point.
void	operator() (result_t &result, double argument) const throw ()
	Evaluate the function at a specified point.
gradient_t	derivative (double argument, size_type order=1) const throw ()
	Compute the derivative of the function.
void	derivative (gradient_t &derivative, double argument, size_type order=1) const throw ()
	Compute the derivative of the function.
virtual std::ostream &	print (std::ostream &o) const throw ()
	Display the function on the specified output stream.
Static Public Attributes
static const size_type	derivabilityOrder = 2
	Function derivability order.
Protected Member Functions
	NTimesDerivableFunction (size_type outputSize=1, std::string name=std::string()) throw ()
	Concrete class constructor should call this constructor.
void	impl_compute (result_t &result, const argument_t &argument) const throw ()
	Function evaluation.
virtual void	impl_compute (result_t &result, double t) const =0 throw ()
	Function evaluation.
void	impl_gradient (gradient_t &gradient, const argument_t &argument, size_type functionId=0) const throw ()
	Gradient evaluation.
virtual void	impl_derivative (gradient_t &derivative, double argument, size_type order=1) const =0 throw ()
	Derivative evaluation.
void	impl_hessian (hessian_t &hessian, const argument_t &argument, size_type functionId=0) const throw ()
	Hessian evaluation.

---

Detailed Description

template<>
class roboptim::NTimesDerivableFunction< 2 >

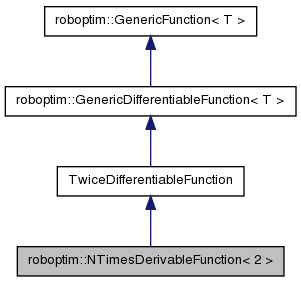
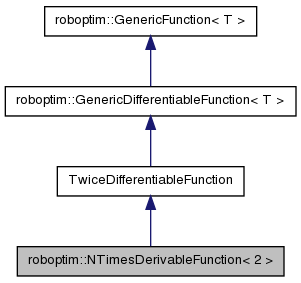
Explicit specialization for the stop case of NTimesDerivable class.

This specialization defines the interface of a ``n times derivable function'' and implements generic methods required by upper classes using this class specific interface.

---

Constructor & Destructor Documentation

virtual roboptim::NTimesDerivableFunction< 2 >::~NTimesDerivableFunction

(

)

throw () [inline, virtual]

roboptim::NTimesDerivableFunction< 2 >::NTimesDerivableFunction	(	size_type	outputSize = 1,
		std::string	name = std::string ()
	)		throw () [inline, protected]

Concrete class constructor should call this constructor.

Parameters:

outputSize	output size (result size)
name	function's name

---

Member Function Documentation

virtual size_type roboptim::NTimesDerivableFunction< 2 >::derivabilityOrderMax

(

)

const [inline, virtual]

Returns the maximum derivability order (relevant for N>2 only)

gradient_t roboptim::NTimesDerivableFunction< 2 >::derivative	(	double	argument,
		size_type	order = 1
	)		const throw () [inline]

Compute the derivative of the function.

Derivative is computed for a certain order, at a given point.

Parameters:

argument	point at which the derivative will be computed
order	derivative order (if 0 then function is evaluated)

Returns:

derivative vector

void roboptim::NTimesDerivableFunction< 2 >::derivative	(	gradient_t &	derivative,
		double	argument,
		size_type	order = 1
	)		const throw () [inline]

Compute the derivative of the function.

Derivative is computed for a certain order, at a given point.

Parameters:

derivative	derivative will be stored in this vector
argument	point at which the derivative will be computed
order	derivative order (if 0 then function is evaluated)

References roboptim::NTimesDerivableFunction< DerivabilityOrder >::derivabilityOrderMax().

size_type roboptim::NTimesDerivableFunction< 2 >::derivativeSize

(

)

const throw () [inline]

Return the size of the derivative vector.

Returns:

derivative vector size

void roboptim::NTimesDerivableFunction< 2 >::impl_compute	(	result_t &	result,
		const argument_t &	argument
	)		const throw () [inline, protected, virtual]

Function evaluation.

Implement generic function evaluation, as required by Function, using this class evaluation method (using a double instead of a vector).

Warning:

Do not call this function directly, call operator()(result_t&, const argument_t&) const throw () instead.

Parameters:

result	result will be stored in this vector
argument	point at which the function will be evaluated

Implements roboptim::GenericFunction< T >.

virtual void roboptim::NTimesDerivableFunction< 2 >::impl_compute	(	result_t &	result,
		double	t
	)		const throw () [protected, pure virtual]

Function evaluation.

Evaluate the function, has to be implemented in concrete classes.

Warning:

Do not call this function directly, call operator()(double) const throw () instead.

Parameters:

result	result will be stored in this vector
t	point at which the function will be evaluated

virtual void roboptim::NTimesDerivableFunction< 2 >::impl_derivative	(	gradient_t &	derivative,
		double	argument,
		size_type	order = 1
	)		const throw () [protected, pure virtual]

Derivative evaluation.

Compute the derivative, has to be implemented in concrete classes.

Warning:

Do not call this function directly, call derivative instead.

Parameters:

derivative	derivative will be store in this argument
argument	point where the gradient will be computed
order	derivative order (if 0 evaluates the function)

void roboptim::NTimesDerivableFunction< 2 >::impl_gradient	(	gradient_t &	gradient,
		const argument_t &	argument,
		size_type	functionId = 0
	)		const throw () [inline, protected, virtual]

Gradient evaluation.

Implement the gradient computation, as required by DerivableFunction. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:

Do not call this function directly, call gradient or derivative instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

Implements roboptim::GenericDifferentiableFunction< T >.

void roboptim::NTimesDerivableFunction< 2 >::impl_hessian	(	hessian_t &	hessian,
		const argument_t &	argument,
		size_type	functionId = 0
	)		const throw () [inline, protected, virtual]

Hessian evaluation.

Implement the hessian computation, as required by the TwiceDerivableFunction class using the derivative method. The hessian is computed for a specific sub-function which id is passed through the functionId argument.

Warning:

Do not call this function directly, call hessian instead.

Parameters:

hessian	hessian will be stored here
argument	point where the hessian will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericTwiceDifferentiableFunction< T >.

bool roboptim::NTimesDerivableFunction< 2 >::isValidDerivative

(

const gradient_t &

derivative

)

const throw () [inline]

Check if a derivative is valid (check sizes).

Parameters:

derivative

derivative vector to be checked

Returns:

true if valid, false if not

result_t roboptim::NTimesDerivableFunction< 2 >::operator()

(

double

argument

)

const throw () [inline]

Evaluate the function at a specified point.

The program will abort if the argument does not have the expected size.

Parameters:

argument

point at which the function will be evaluated

Returns:

computed result

void roboptim::NTimesDerivableFunction< 2 >::operator()	(	result_t &	result,
		double	argument
	)		const throw () [inline]

Evaluate the function at a specified point.

The program will abort if the argument does not have the expected size.

Parameters:

result	result will be stored in this vector
argument	point at which the function will be evaluated

Returns:

computed result

virtual std::ostream& roboptim::NTimesDerivableFunction< 2 >::print

(

std::ostream &

o

)

const throw () [inline, virtual]

Display the function on the specified output stream.

Parameters:

o	output stream used for display

Returns:

output stream

Reimplemented from roboptim::GenericTwiceDifferentiableFunction< T >.

References roboptim::NTimesDerivableFunction< DerivabilityOrder >::derivabilityOrderMax().

---

Member Data Documentation

const size_type roboptim::NTimesDerivableFunction< 2 >::derivabilityOrder = 2 [static]

Function derivability order.

One static const variable per class in inheritance structure.