Compute automatically a gradient with finite differences. More...
#include <roboptim/core/decorator/finite-difference-gradient.hh>
Public Member Functions | |
| ROBOPTIM_DIFFERENTIABLE_FUNCTION_FWD_TYPEDEFS_ (GenericDifferentiableFunction< T >) | |
| GenericFiniteDifferenceGradient (const GenericFunction< T > &f, value_type e=finiteDifferenceEpsilon) | |
| Instantiate a finite differences gradient. | |
| ~GenericFiniteDifferenceGradient () | |
Protected Member Functions | |
| virtual void | impl_compute (result_ref, const_argument_ref) const |
| Function evaluation. | |
| virtual void | impl_gradient (gradient_ref, const_argument_ref argument, size_type=0) const |
| Gradient evaluation. | |
| virtual void | impl_jacobian (jacobian_ref jacobian, const_argument_ref argument) const |
| Jacobian evaluation. | |
Protected Attributes | |
| const GenericFunction< T > & | adaptee_ |
| Reference to the wrapped function. | |
| const value_type | epsilon_ |
| argument_t | xEps_ |
Compute automatically a gradient with finite differences.
Finite difference gradient is a method to approximate a function's gradient. It is particularly useful in RobOptim to avoid the need to compute the analytical gradient manually.
This class takes a Function as its input and wraps it into a derivable function.
The one dimensional formula is:
![\[f'(x)\approx {f(x+\epsilon)-f(x)\over \epsilon}\]](form_0.png)
where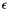 
is a constant given when calling the class constructor.
| roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::GenericFiniteDifferenceGradient | ( | const GenericFunction< T > & | f, |
| value_type | e = finiteDifferenceEpsilon |
||
| ) |
Instantiate a finite differences gradient.
Instantiate a derivable function that will wraps a non derivable function and compute automatically its gradient using finite differences.
| f | function that will e wrapped |
| e | epsilon used in finite difference computation |
| roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::~GenericFiniteDifferenceGradient | ( | ) |
| void roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::impl_compute | ( | result_ref | result, |
| const_argument_ref | argument | ||
| ) | const [protected, virtual] |
Function evaluation.
Evaluate the function, has to be implemented in concrete classes.
| result | result will be stored in this vector |
| argument | point at which the function will be evaluated |
Implements roboptim::GenericFunction< T >.
| void roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::impl_gradient | ( | gradient_ref | gradient, |
| const_argument_ref | argument, | ||
| size_type | functionId = 0 |
||
| ) | const [protected, virtual] |
Gradient evaluation.
Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.
| gradient | gradient will be store in this argument |
| argument | point where the gradient will be computed |
| functionId | evaluated function id in the split representation |
Implements roboptim::GenericDifferentiableFunction< T >.
| void roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::impl_jacobian | ( | jacobian_ref | jacobian, |
| const_argument_ref | arg | ||
| ) | const [protected, virtual] |
Jacobian evaluation.
Computes the jacobian, can be overridden by concrete classes. The default behavior is to compute the jacobian from the gradient.
| jacobian | jacobian will be store in this argument |
| arg | point where the jacobian will be computed |
Reimplemented from roboptim::GenericDifferentiableFunction< T >.
| roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::ROBOPTIM_DIFFERENTIABLE_FUNCTION_FWD_TYPEDEFS_ | ( | GenericDifferentiableFunction< T > | ) |
const GenericFunction<T>& roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::adaptee_ [protected] |
Reference to the wrapped function.
const value_type roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::epsilon_ [protected] |
argument_t roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >::xEps_ [mutable, protected] |
