roboptim::GenericNumericQuadraticFunction< T > Class Template Reference

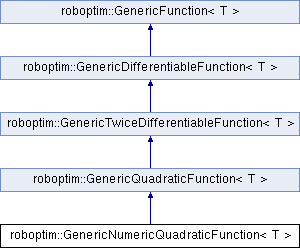
Build a quadratic function from a matrix and a vector. More...

#include <roboptim/core/numeric-quadratic-function.hh>

Inheritance diagram for roboptim::GenericNumericQuadraticFunction< T >:

List of all members.

Public Types
typedef matrix_t	symmetric_t
	Symmetric matrix type.
Public Member Functions
	ROBOPTIM_TWICE_DIFFERENTIABLE_FUNCTION_FWD_TYPEDEFS_ (GenericQuadraticFunction< T >)
	GenericNumericQuadraticFunction (const symmetric_t &A, const vector_t &b)
	Build a quadratic function from a matrix and a vector.
	GenericNumericQuadraticFunction (const symmetric_t &A, const vector_t &b, const vector_t &c)
	Build a quadratic function from a matrix and a vector.
	~GenericNumericQuadraticFunction ()
virtual std::ostream &	print (std::ostream &) const
	Display the function on the specified output stream.
const matrix_t &	A () const
const vector_t &	b () const
const vector_t &	c () const
matrix_t &	A ()
vector_t &	b ()
vector_t &	c ()
Protected Member Functions
void	impl_compute (result_ref, const_argument_ref) const
	Function evaluation.
void	impl_gradient (gradient_ref, const_argument_ref, size_type=0) const
	Gradient evaluation.
void	impl_jacobian (jacobian_ref, const_argument_ref) const
	Jacobian evaluation.
void	impl_hessian (hessian_ref hessian, const_argument_ref argument, size_type functionId=0) const
	Hessian evaluation.
template<>
void	impl_jacobian (jacobian_ref jacobian, const_argument_ref x) const
	Jacobian evaluation.
template<>
void	impl_gradient (gradient_ref gradient, const_argument_ref x, size_type) const
	Gradient evaluation.

---

Detailed Description

template<typename T>
class roboptim::GenericNumericQuadraticFunction< T >

Build a quadratic function from a matrix and a vector.

Implement a quadratic function using the general formula:

where 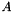and 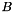are set when the class is instantiated.

Note:

A is a symmetric matrix.

Examples:

numeric-quadratic-function.cc.

---

Member Typedef Documentation

template<typename T>

typedef matrix_t roboptim::GenericNumericQuadraticFunction< T >::symmetric_t

Symmetric matrix type.

---

Constructor & Destructor Documentation

template<typename T >

roboptim::GenericNumericQuadraticFunction< T >::GenericNumericQuadraticFunction	(	const symmetric_t &	A,
		const vector_t &	b
	)

Build a quadratic function from a matrix and a vector.

c here is omitted and set to zero.

See class documentation for A and b definition.

Parameters:

A	A symmetric matrix
b	b vector

References roboptim::GenericTwiceDifferentiableFunction< T >::setZero().

template<typename T >

roboptim::GenericNumericQuadraticFunction< T >::GenericNumericQuadraticFunction	(	const symmetric_t &	A,
		const vector_t &	b,
		const vector_t &	c
	)

Build a quadratic function from a matrix and a vector.

See class documentation for A, b, c definition.

Parameters:

A	A symmetric matrix (inputSize * inputSize)
b	b vector (size inputSize)
c	c vector (size one)

template<typename T >

roboptim::GenericNumericQuadraticFunction< T >::~GenericNumericQuadraticFunction

(

)

---

Member Function Documentation

template<typename T>

const matrix_t& roboptim::GenericNumericQuadraticFunction< T >::A

(

)

const [inline]

template<typename T>

matrix_t& roboptim::GenericNumericQuadraticFunction< T >::A

(

)

[inline]

template<typename T>

const vector_t& roboptim::GenericNumericQuadraticFunction< T >::b

(

)

const [inline]

template<typename T>

vector_t& roboptim::GenericNumericQuadraticFunction< T >::b

(

)

[inline]

template<typename T>

const vector_t& roboptim::GenericNumericQuadraticFunction< T >::c

(

)

const [inline]

template<typename T>

vector_t& roboptim::GenericNumericQuadraticFunction< T >::c

(

)

[inline]

template<typename T >

void roboptim::GenericNumericQuadraticFunction< T >::impl_compute	(	result_ref	result,
		const_argument_ref	argument
	)		const [protected, virtual]

Function evaluation.

Evaluate the function, has to be implemented in concrete classes.

Warning:

Do not call this function directly, call operator()(result_ref, const_argument_ref) const instead.

Parameters:

result	result will be stored in this vector
argument	point at which the function will be evaluated

Implements roboptim::GenericFunction< T >.

template<>

void roboptim::GenericNumericQuadraticFunction< EigenMatrixSparse >::impl_gradient	(	gradient_ref	gradient,
		const_argument_ref	argument,
		size_type	functionId
	)		const [inline, protected, virtual]

Gradient evaluation.

Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:

Do not call this function directly, call gradient instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::GenericNumericQuadraticFunction< T >::impl_gradient	(	gradient_ref	gradient,
		const_argument_ref	argument,
		size_type	functionId = 0
	)		const [protected, virtual]

Gradient evaluation.

Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:

Do not call this function directly, call gradient instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::GenericNumericQuadraticFunction< T >::impl_hessian	(	hessian_ref	hessian,
		const_argument_ref	argument,
		size_type	functionId = 0
	)		const [protected, virtual]

Hessian evaluation.

Compute the hessian, has to be implemented in concrete classes. The hessian is computed for a specific sub-function which id is passed through the functionId argument.

Warning:

Do not call this function directly, call hessian instead.

Parameters:

hessian	hessian will be stored here
argument	point where the hessian will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericTwiceDifferentiableFunction< T >.

template<>

void roboptim::GenericNumericQuadraticFunction< EigenMatrixSparse >::impl_jacobian	(	jacobian_ref	jacobian,
		const_argument_ref	arg
	)		const [inline, protected, virtual]

Jacobian evaluation.

Computes the jacobian, can be overridden by concrete classes. The default behavior is to compute the jacobian from the gradient.

Warning:

Do not call this function directly, call jacobian instead.

Parameters:

jacobian	jacobian will be store in this argument
arg	point where the jacobian will be computed

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

Reimplemented from roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::GenericNumericQuadraticFunction< T >::impl_jacobian	(	jacobian_ref	jacobian,
		const_argument_ref	arg
	)		const [protected, virtual]

Jacobian evaluation.

Computes the jacobian, can be overridden by concrete classes. The default behavior is to compute the jacobian from the gradient.

Warning:

Do not call this function directly, call jacobian instead.

Parameters:

jacobian	jacobian will be store in this argument
arg	point where the jacobian will be computed

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

Reimplemented from roboptim::GenericDifferentiableFunction< T >.

template<typename T >

std::ostream & roboptim::GenericNumericQuadraticFunction< T >::print

(

std::ostream &

o

)

const [virtual]

Display the function on the specified output stream.

Parameters:

o	output stream used for display

Returns:

output stream

Reimplemented from roboptim::GenericQuadraticFunction< T >.

References roboptim::decindent(), roboptim::iendl(), and roboptim::incindent().

template<typename T>

roboptim::GenericNumericQuadraticFunction< T >::ROBOPTIM_TWICE_DIFFERENTIABLE_FUNCTION_FWD_TYPEDEFS_

(

GenericQuadraticFunction< T >

)