Classes
class	roboptim::GenericFiniteDifferenceGradient< T, FdgPolicy >
	Compute automatically a gradient with finite differences. More...
class	roboptim::GenericConstantFunction< T >
	Constant function. More...
class	roboptim::Cos< T >
	Cos function. More...
class	roboptim::GenericIdentityFunction< T >
	Identity function. More...
class	roboptim::Polynomial< T >
	Polynomial function. More...
class	roboptim::Sin< T >
	Sin function. More...
class	roboptim::NTimesDerivableFunction< 2 >
	Explicit specialization for the stop case of NTimesDerivable class. More...
class	roboptim::NTimesDerivableFunction< DerivabilityOrder >
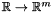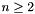	Define a $\mathbb{R} \rightarrow \mathbb{R}^m$ function, derivable n times ( $n \geq 2$ ). More...
class	roboptim::GenericNumericLinearFunction< T >
	Build a linear function from a vector and a matrix. More...
class	roboptim::GenericNumericQuadraticFunction< T >
	Build a quadratic function from a matrix and a vector. More...
Functions
template<typename T >
bool	roboptim::checkGradient (const GenericDifferentiableFunction< T > &function, typename GenericDifferentiableFunction< T >::size_type functionId, typename GenericDifferentiableFunction< T >::const_argument_ref x, typename GenericDifferentiableFunction< T >::value_type threshold=finiteDifferenceThreshold)
	Check if a gradient is valid.
template<typename T >
void	roboptim::checkGradientAndThrow (const GenericDifferentiableFunction< T > &function, typename GenericDifferentiableFunction< T >::size_type functionId, typename GenericDifferentiableFunction< T >::const_argument_ref x, typename GenericDifferentiableFunction< T >::value_type threshold=finiteDifferenceThreshold) throw (BadGradient<T>)
template<typename T >
bool	roboptim::checkJacobian (const GenericDifferentiableFunction< T > &function, typename GenericDifferentiableFunction< T >::const_argument_ref x, typename GenericDifferentiableFunction< T >::value_type threshold=finiteDifferenceThreshold)
	Check if a Jacobian is valid.
template<typename T >
void	roboptim::checkJacobianAndThrow (const GenericDifferentiableFunction< T > &function, typename GenericDifferentiableFunction< T >::const_argument_ref x, typename GenericDifferentiableFunction< T >::value_type threshold=finiteDifferenceThreshold) throw (BadJacobian<T>)
void	roboptim::Cos< T >::impl_gradient (gradient_ref gradient, const_argument_ref x, size_type) const
	Gradient evaluation.
void	roboptim::Cos< T >::impl_jacobian (jacobian_ref jacobian, const_argument_ref x) const
	Jacobian evaluation.
void	roboptim::Cos< T >::impl_hessian (hessian_ref hessian, const_argument_ref x, size_type) const
	Hessian evaluation.
void	roboptim::GenericIdentityFunction< T >::impl_gradient (gradient_ref gradient, const_argument_ref, size_type idFunction) const
	Gradient evaluation.
void	roboptim::Sin< T >::impl_gradient (gradient_ref gradient, const_argument_ref x, size_type) const
	Gradient evaluation.
void	roboptim::Sin< T >::impl_jacobian (jacobian_ref jacobian, const_argument_ref x) const
	Jacobian evaluation.
void	roboptim::Sin< T >::impl_hessian (hessian_ref hessian, const_argument_ref x, size_type) const
	Hessian evaluation.

Function Documentation

template<typename T >

bool roboptim::checkGradient	(	const GenericDifferentiableFunction< T > &	function,
		typename GenericDifferentiableFunction< T >::size_type	functionId,
		typename GenericDifferentiableFunction< T >::const_argument_ref	x,
		typename GenericDifferentiableFunction< T >::value_type	threshold = `finiteDifferenceThreshold`
	)

Check if a gradient is valid.

Check if a gradient is valid by comparing the distance between its gradient and an automatically computed finite differences gradient.

Parameters:

function	function that will be checked
functionId	function id in split representation
x	point where the gradient will be evaluated
threshold	maximum tolerated error

Returns:: true if valid, false if not

Examples:: finite-difference-gradient.cc, and numeric-quadratic-function.cc.

References roboptim::allclose(), and roboptim::GenericDifferentiableFunction< T >::gradient().

Referenced by roboptim::checkGradientAndThrow().

template<typename T >

void roboptim::checkGradientAndThrow	(	const GenericDifferentiableFunction< T > &	function,
		typename GenericDifferentiableFunction< T >::size_type	functionId,
		typename GenericDifferentiableFunction< T >::const_argument_ref	x,
		typename GenericDifferentiableFunction< T >::value_type	threshold = `finiteDifferenceThreshold`
	)		throw (BadGradient<T>)

Examples:: finite-difference-gradient.cc.

References roboptim::checkGradient(), and roboptim::GenericDifferentiableFunction< T >::gradient().

template<typename T >

bool roboptim::checkJacobian	(	const GenericDifferentiableFunction< T > &	function,
		typename GenericDifferentiableFunction< T >::const_argument_ref	x,
		typename GenericDifferentiableFunction< T >::value_type	threshold = `finiteDifferenceThreshold`
	)

Check if a Jacobian is valid.

Check if a Jacobian is valid by comparing the distance between the matrix and an automatically computed finite differences Jacobian.

Parameters:

function	function that will be checked
x	point where the Jacobian will be evaluated
threshold	maximum tolerated error

Returns:: true if valid, false if not

Examples:: numeric-quadratic-function.cc.

References roboptim::allclose(), and roboptim::GenericDifferentiableFunction< T >::jacobian().

Referenced by roboptim::checkJacobianAndThrow().

template<typename T >

void roboptim::checkJacobianAndThrow	(	const GenericDifferentiableFunction< T > &	function,
		typename GenericDifferentiableFunction< T >::const_argument_ref	x,
		typename GenericDifferentiableFunction< T >::value_type	threshold = `finiteDifferenceThreshold`
	)		throw (BadJacobian<T>)

Examples:: finite-difference-gradient.cc.

References roboptim::checkJacobian(), and roboptim::GenericDifferentiableFunction< T >::jacobian().

template<typename T >

void roboptim::Sin< T >::impl_gradient	(	gradient_ref	gradient,
		const_argument_ref	argument,
		size_type	functionId
	)		const `[protected, virtual]`

Gradient evaluation.

Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:: Do not call this function directly, call gradient instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::Cos< T >::impl_gradient	(	gradient_ref	gradient,
		const_argument_ref	argument,
		size_type	functionId
	)		const `[protected, virtual]`

Gradient evaluation.

Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:: Do not call this function directly, call gradient instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::GenericIdentityFunction< T >::impl_gradient	(	gradient_ref	gradient,
		const_argument_ref	argument,
		size_type	functionId
	)		const `[protected, virtual]`

Gradient evaluation.

Compute the gradient, has to be implemented in concrete classes. The gradient is computed for a specific sub-function which id is passed through the functionId argument.

Warning:: Do not call this function directly, call gradient instead.

Parameters:

gradient	gradient will be store in this argument
argument	point where the gradient will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::Sin< T >::impl_hessian	(	hessian_ref	hessian,
		const_argument_ref	argument,
		size_type	functionId
	)		const `[protected, virtual]`

Hessian evaluation.

Compute the hessian, has to be implemented in concrete classes. The hessian is computed for a specific sub-function which id is passed through the functionId argument.

Warning:: Do not call this function directly, call hessian instead.

Parameters:

hessian	hessian will be stored here
argument	point where the hessian will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericTwiceDifferentiableFunction< T >.

template<typename T >

void roboptim::Cos< T >::impl_hessian	(	hessian_ref	hessian,
		const_argument_ref	argument,
		size_type	functionId
	)		const `[protected, virtual]`

Hessian evaluation.

Compute the hessian, has to be implemented in concrete classes. The hessian is computed for a specific sub-function which id is passed through the functionId argument.

Warning:: Do not call this function directly, call hessian instead.

Parameters:

hessian	hessian will be stored here
argument	point where the hessian will be computed
functionId	evaluated function id in the split representation

Implements roboptim::GenericTwiceDifferentiableFunction< T >.

template<typename T >

void roboptim::Sin< T >::impl_jacobian	(	jacobian_ref	jacobian,
		const_argument_ref	arg
	)		const `[protected, virtual]`

Jacobian evaluation.

Computes the jacobian, can be overridden by concrete classes. The default behavior is to compute the jacobian from the gradient.

Warning:: Do not call this function directly, call jacobian instead.

Parameters:

jacobian	jacobian will be store in this argument
arg	point where the jacobian will be computed

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

Reimplemented from roboptim::GenericDifferentiableFunction< T >.

template<typename T >

void roboptim::Cos< T >::impl_jacobian	(	jacobian_ref	jacobian,
		const_argument_ref	arg
	)		const `[protected, virtual]`

Jacobian evaluation.

Computes the jacobian, can be overridden by concrete classes. The default behavior is to compute the jacobian from the gradient.

Warning:: Do not call this function directly, call jacobian instead.

Parameters:

jacobian	jacobian will be store in this argument
arg	point where the jacobian will be computed

ROBOPTIM_DO_NOT_CHECK_ALLOCATION

Reimplemented from roboptim::GenericDifferentiableFunction< T >.

Classes

Functions

Function Documentation